JERARQUIA DE LOS CONECTORES LOGICOS

JERARQUIA DE LOS CONECTORES LOGICOS

La jerarquía de operadores es el orden en el que se resolverá una expresión compuesta, y el orden es el siguiente.

Primero que nada los operadores del mismo orden se resuelven de izquierda a derecha.

1.-Paréntesis  ().

2.-Operadores unarios.

3.-Operadores binarios.

Ejemplo 1 .

(r^s) ^ p → ¬ q

p	q	r	s	(r^s)	¬q	(r^s)^p	(r^s) ^ p → ¬ q
V	V	V	V	V	F	V	F
V	V	V	F	F	F	F	V
V	V	F	V	F	F	F	V
V	V	F	F	F	F	F	V
V	F	V	V	V	V	V	V
V	F	V	F	F	V	F	V
V	F	F	V	F	V	F	V
V	F	F	F	F	V	F	V
F	V	V	V	V	F	F	V
F	V	V	F	F	F	F	V
F	V	F	V	F	F	F	V
F	V	F	F	F	F	F	V
F	F	V	V	V	V	F	V
F	F	V	F	F	V	F	V
F	F	F	V	F	V	F	V
F	F	F	F	F	V	F	V

 

CONECTORES LOGICOS Y TABLAS DE VERDAD

CONECTIVA LÓGICA

Las conectivas son funciones de verdad. Quiere decir que son funciones que toman uno o dos valores de verdad, y devuelven un único valor de verdad. En consecuencia, cada conectiva lógica puede ser definida mediante una tabla de valores de verdad que indique qué valor devuelve la conectiva para cada combinación de valores de verdad. A continuación hay una tabla con las conectivas más usuales y su definición mediante tablas de verdad:

 

Conectiva	Notación	Ejemplo de uso	Análogo natural	Ejemplo de uso en el lenguaje natural	Tabla de verdad
Negación		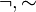	no	No está lloviendo.
Conjunción			y	Está lloviendo y es de noche.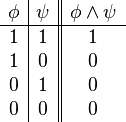
Disyunción			o	Está lloviendo o es de noche.
Condicional		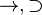	si... entonces	Si está lloviendo, entonces es de noche.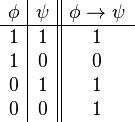
Bicondicional			si y sólo si	Está lloviendo si y sólo si es de noche.